I am building an open world game which happens on an earth-like planet. At the beginning, I tried to generate the planet with voxels at the run-time, like Minecraft. The benefit of this approach is we don’t need to keep everything in memory, only the visible chunks. The drawback is it’s difficult to get a overview of the whole planet, to generate meaningful regions for providing a strategic gameplay.
So I took a step back and continued on a Voronoi based approach. There are already similar techniques existing. Polygonal Map Generation for Games from Red Blob Games is a great article about that. However, there are some important differences in this implementation.
Spherical Voronoi
The first step of the map generation is to create polygons. If on a plane, we could use the Fortune’s algorithm, which creates the Voronoi diagram in O(n log n) time and O(n) space complexity. On spherical surface, we could use a similar approach, by sweeping the surface from the north pole to south pole. Although the data structure and mathematics is more complicated, the entire algorithm is not that difficult as the first instinct. Since the spherical surface is within a closed space, there are less edge conditions to deal with.
We don’t want to generate the Voronoi diagram from random points. It would create a very irregular polygon mesh. Instead of that, I started from a distance-corrected cube sphere projection, subdivided each cube face to 1024 regions, and place the Voronoi cell centers on random positions inside each region.
I built my Spherical Voronoi generation based on the algorithm described in this paper: A Plane Sweep Algorithm for the Voronoi Tessellation of the Sphere. You may find the essential codes on Github.
The generated Voronoi looks like this:
Altitude, Ocean and Lakes
The altitudes are generated from an octave Perlin noise, sampled on each Voronoi center and corner. If a cell center’s altitude is below the ocean level, it will become a water cell.
All the water cells are grouped. The groups are sorted according to the number of cells it includes. In the groups those contains a big amount of cells, they will be marked as ocean (salted water). And the small groups will be marked as lake (fresh water).
Generate Rivers
Rivers are generated on the Voronoi borders. For each vertex, we find the downhill border by link it to the lowest vertex among its neighbours. If all the neighbour vertices is above it, or has the same altitude, the downhill border is null. We also set the uphill border as the opposite of the downhill border, i.e.:
vertex->m_downHillBorder->m_endCorner->m_upHillBorder = vertex->m_downHillBorder;
To generate the rivers, we randomly pick a vertex on the land cells of the Voronoi graph, and follow the uphill border until the end, unless it may intersect with another generated river. From where, we generate the river through the downhill borders, until it reaches a water cell. We repeat the procedure several times. Sometime rivers could merge. We increase the border’s water_amount attribute to represent it.
Moisture
With the entire river system generated, we could then compute the moisture level of each cell. The base moisture level for each cell is like this:
+-------+--------------+
| Ocean | 0.5 |
| Lake | 1.0 |
| River | (amount*0.5) |
+-------+--------------+
After setting the base moisture, we perform several iterations to propagate the moisture to neighbour cells. The propagate amount is affected by the attitude difference of neighbour cells. The less difference in the attitude, the more moisture is propagated.
const int nbIterations = 8;
for (int iter=0; iter < nbIterations; ++iter)
{
for (size_t i = 0; i < m_planetVoronoiCenters.size(); ++ i)
{
auto& c = m_planetVoronoiCenters[i].get();
Real totalAmount = (moistures[i] + baseMoistures[i]) * 0.5;
Real totalWeight = 1;
for (auto pNeighbour : c.m_neighbourCenters)
{
Real diffHeight = glm::abs(c.relativeHeight() - pNeighbour->relativeHeight()) * 0.5;
Real weight = (1.0 - diffHeight);
totalAmount += moistures[pNeighbour->m_cell->index] * weight;
totalWeight += weight;
}
tempResult[i] = totalAmount / totalWeight;
}
std::copy(tempResult.begin(), tempResult.end(), moistures.begin());
}
for (size_t i = 0; i < m_planetVoronoiCenters.size(); ++i)
{
m_planetVoronoiCenters[i].get().m_moisture = moistures[i];
}
After that, we preform another pass to compute the moisture on each Voronoi vertex by interpolating the moisture on all neighbour cell centers. Here is how the interpolation function works:
Real interpolateSphericalSamples(const Point& p0, const std::vector<Point>& points, const std::vector<Real>& values)
{
Real totalSqrDistance = std::accumulate(points.begin(), points.end(), 0.0, [p0](Real res, const Point& p) {
Real d = p.sphericalDistance(p0);
return res + d * d;
});
Real sum = 0.0;
Real weight = 0.0;
for (size_t i = 0; i < points.size(); ++i)
{
const Point& p = points[i];
Real d = p.sphericalDistance(p0);
Real w = (totalSqrDistance - d*d) / totalSqrDistance;
sum += w * values[i];
weight += w;
}
return sum / weight;
}
And here is the moisture distribution map:

Temperature
Similar with the moisture level, we compute the base temperature of each cell by considering both their latitudes and their altitudes. After that we propagate the temperate to neighbour cells not only considering the altitude differences, but also if they are water or land cells:
auto& c = m_planetVoronoiCenters[i].get();
Real totalAmount = (temperatures[i] + baseTemperatures[i]) * 0.5;
Real totalWeight = 1;
for (auto pNeighbour : c.m_neighbourCenters)
{
float weight;
if (c.isWater() && pNeighbour->isWater())
{
weight = 0.75;
}
else if (!c.isWater() && !pNeighbour->isWater())
{
weight = 0.25;
}
else
{
weight = 0.5;
}
float diffHeight = glm::abs(c.relativeHeight() - pNeighbour->relativeHeight());
weight *= (1.0 - diffHeight);
totalAmount += temperatures[pNeighbour->m_cell->index] * weight;
totalWeight += weight;
}
tempResult[i] = totalAmount / totalWeight;
From the picture, we could see how the temperature is modified by the altitude and latitude, and how the temperature propagates on lands and waters.
Biome types
For each Voronoi cell, we could find its biome type with this table (Biome : Wikipedia):
Also we apply the following palette for each biome type

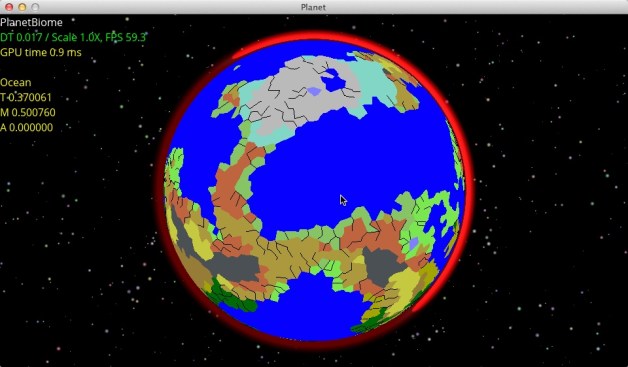
Here are the final results:
 Another side of the planet:
Another side of the planet: Close to the north pole:
Close to the north pole:
Close to the south pole:
Finally, a demo video:
References
[1] Polygonal Map Generation for Games
[2] A Plane Sweep Algorithm for the Voronoi Tessellation of the Sphere
[3] Biome : Wikipedia
[4] Essential code for generating spherical Voronoi